How To Find A Intersection B In Sets

Intersection of sets

This lesson volition explicate how to detect the intersection of sets. We will first with a definition of the intersection of two sets.

Definition:

Given 2 sets A and B, the intersection is the set that contains elements or objects that belong to A and to B at the same time.

Nosotros write A ∩ B

Basically, we find A ∩ B past looking for all the elements A and B take in mutual. Next, we illustrate with examples.

Case #i.

To arrive piece of cake, detect that what they take in common is in assuming.

Allow A = { i orange , 1 pineapple, i banana, i apple } and B = { 1 spoon, 1 orange , 1 pocketknife, 1 fork, 1 apple }

A ∩ B = { one orange, one apple }

Example #ii.

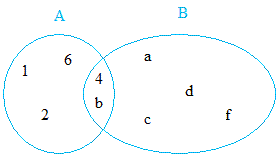
Notice the intersection of A and B and and so brand a Venn diagrams.

A = {b, one, 2, 4, 6 } and B = { four, a, b, c, d, f }

A ∩ B = { iv, b }

Intersection of A and B

Example #iii.

A = { x / x is a number bigger than four and smaller than 8 }

B = { x / x is a positive number smaller than 7 }

A = { v, half-dozen, 7 } and B = { 1, ii, 3, 4, 5, half-dozen}

A ∩ B = { 5, 6 }

Or A ∩ B = { x / x is a number bigger than iv and smaller than vii }

Example #iv.

A = { ten / x is a state in Asia }

B = { 10 / x is a country in Africa }

Since no countries in Asia and Africa are the aforementioned, the intersection is empty.

A ∩ B = { }

Instance #five.

Intersection of sets

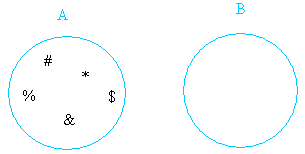
A = { #, %, &,

*, $ }

B = { }

This instance is subtle! Since the empty set is included in whatsoever set, it is also included in A although you don't see it.

Therefore, the empty gear up is the simply thing set A and set B have in common.

A ∩ B = { }

In fact, since the empty set up is included in any ready, the intersection of the empty ready with any set is the empty set.

Definition of the union of three sets:

Given three sets A, B, and C the intersection is the set that contains elements or objects that belong to A, B, and to C at the same time.

Nosotros write A ∩ B ∩ C

Basically, we detect A ∩ B ∩ C by looking for all the elements A, B, and C have in common.

A = { #, i, 2, 4, 6 }, B = { #, a, b, 4, c } and C = A = { #, %, &, *, $, 4 }

A ∩ B ∩ C = { 4 , # }

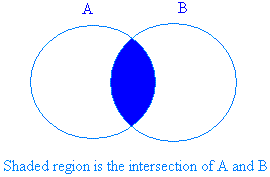
The graph beneath shows the shaded region for the intersection of two sets

Intersection of A and B

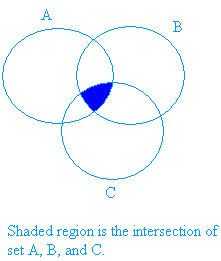
The graph below shows the shaded region for the intersection of three sets

Intersection of 3 sets

This ends the lesson virtually intersection of sets. If yous have any questions nigh the intersection of sets, I will be more than than happy to respond them.

Use the quiz below to run across how well you can detect the intersection of sets.